2023. 5. 26. 18:20ㆍ프로그래밍 자료 조사
1. 벡터
벡터의 정의
벡터 : 크기와 방향의 두 요소를 가지는 양으로, 물체의 운동속도나 작용하는 힘을 나타낼 수 있다.
벡터의 표기법:
A에서 B로 향하는 화살표를 이용하여 크기와 방향을 나타내고,
기호로는 $\vec{AB}$ 또는 $\vec{a}$로 표기하고
점 A를 위 벡터의 시점, B를 종점이라고 한다.

벡터의 크기 :
AB의 길이를 벡터에서는 크기라 하고,
기호로는 $|\vec{AB}|$ 로 나타낸다.
이중에서 크기가 1인 벡터는 단위벡터라고 부르고, 시점과 종점이 같은 벡터는 크기가 0이므로 영벡터라 한다.

서로 같은 벡터
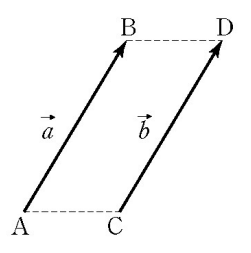
위 그림과 같이 벡터의 크기와 방향이 같을 때, 두 벡터는 서로 같다고 하며
위치는 다르더라도 벡터의 개념상 같기 때문에 평행이동 하여 겹칠 수 있다.
2. 단위 벡터 (Unit vectors)

3. 벡터의 스칼라

4. 벡터의 정규화

5. 벡터의 합연산

6. 벡터의 곱연산

7. 벡터의 내적
내적은 scalar product(스칼라 곱) 또는 dot product라고도 하며 기호로 •(dot)을 사용한다. 벡터의 내적을 이용해 두 벡터 사이의 각을 구할 수 있다.
내적을 구하는 두가지 방법 :
1. 벡터의 각 성분값을 곱하여 더하는 것
A • B = (Ax * Bx) + (Ay * By)
2. 두 벡터의 크기를 곱하는 것
<u, v> = u • v = |u||v|cosθ
8. 벡터의 외적
벡터의 내적, 외적이라고 이름만 비슷하지 서로 전혀 다른 연산이다. 'A ⨉ B'로 표현하며, 두 개의 벡터에 수직하는 벡터의 방향과 크기를 구할 수 있다.
A ⨉ B = (AyBz - AzBy, AzBx - AxBz, AxBy-AyBx)
'프로그래밍 자료 조사' 카테고리의 다른 글
| push_back 과 emplace_back의 차이 (0) | 2023.10.24 |
|---|---|
| STL MAP 자료조사 (0) | 2023.06.28 |
| 행렬 (0) | 2023.05.24 |
| 추상클래스 & 인터페이스 클래스 (0) | 2023.05.19 |
| 삼각함수 공부 (0) | 2023.05.15 |